Выбор оптимальных параметров системы управления высотой полёта

Выберем =0.8 c

Была составлена программа в пакете Matlab

Для переходного процесса с перерегулированием (ξ=0.707)

clc

syms x y iteta ih

V=265.68;

H=11000;

cdteta=0.645;

cdalpha=0.105;

calpha=2.63;

balpha=0.632;

cv=29.275;

idteta=0.8;

ksi=0.707;

tp=21;

tau2=tp/3;

a0=1;

a1=cdteta+cdalpha+balpha+cv*idteta

A=balpha*(cdteta+cv*idteta)+calpha

Res=solve((a1*x*((x*y)^0.25))/(tau2)+((1-(a1/balpha))*((1+x-y)/(tau2^2))*sqrt(x*y))-x*(x-y)*A,1-x-y);

x=double(Res.x);

y=double(Res.y);

tt=find(x>0&y>0&x-y>0&x+y<=1&imag(x)==0);

x=x(tt)

y=y(tt)

a3=(a1*(1+x-y)*sqrt(x*y))/((tau2^2)*x*(x-y))

a4=(a1*(x*y)^0.75)/((tau2^3)*x*(x-y))

a2=(a3/balpha)+A

В итоге получили следующие результаты:

;

;

;

.

По известным коэффициентам из системы (7.4) нашли передаточные числа автопилота:

;

c;

град/м.

Необходимо знать, имеют ли место нули в числителе передаточной функции. Нули в числителе могут увеличить время переходного процесса. Чтобы узнать о наличии нулей в числителе запишем частный определитель:

.

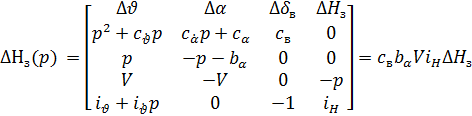Таким образом, передаточная функция запишется в следующем виде:

.(9.14)

Как видно из формулы (9.14) нулей в числителе передаточной функции нет.

На рисунке (9.1) представлен график переходного процесса системы (9.14)

На управляющее воздействие =60м

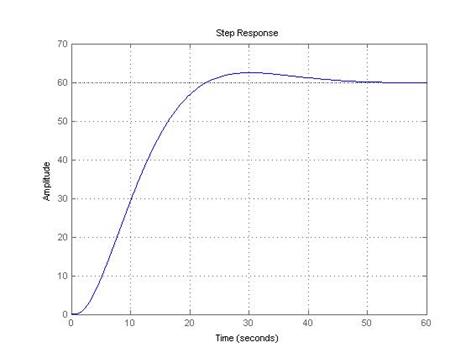
Рис 9.1

Как видно из рис 9.1 время регулирования по высоте полета равно 21с. Таким образом, мы обеспечили необходимое качество регулирования высоты полета.

Для переходного процесса без перерегулирования (ξ=1)

clc

syms x y iteta ih

V=265.68;

H=11000;

cdteta=0.645;

cdalpha=0.105;

calpha=2.63;

balpha=0.632;

cv=29.275;

ksi=1;

xp=0.5;

a0=1;

idteta=0.4;

tp=20

a1=cdteta+cdalpha+balpha+cv*idteta

tau2=tp/4.74

A=balpha*(cdteta+cv*idteta)+calpha

Res=solve((a1*x*((x*y)^0.25))/(tau2)+((1-(a1/balpha))*((1+x-y)/(tau2^2))*sqrt(x*y))-x*(x-y)*A,-y+((sqrt(x)-1)^2));

x=double(Res.x);

y=double(Res.y);

tt=find(x>0&y>0&x-y>0&x+y<=1&imag(x)==0);

x=x(tt)

y=y(tt)

a3=(a1*(1+x-y)*sqrt(x*y))/((tau2^2)*x*(x-y))

a4=(a1*(x*y)^0.75)/((tau2^3)*x*(x-y))

В итоге получили следующие результаты:

;

;

;

.

По известным коэффициентам из системы (7.4) нашли передаточные числа автопилота:

Похожие статьи:

Параметры функции плотности распределения отказов
Делаем предположение, что по виду полигона данное распределение отказов описывается экспоненциальной функцией: (3.1) Эта функция, определяющая скорость нарастания отказов, является однопараметровой, т. к. зависит только от интенсивности потока отказов l: (3.2) Интенсивность потока отказов: - для вн ...

Метод расчета и расчетные усилия
Расчет выполняется методом конечных элементов машинным способом в конечно-элементном пакете ИСПА (Интегрированная Система Прочностного Анализа). В качестве расчетных усилий приняты нагрузки, предоставленные 52 отделом – смотри рисунок 1 (лист 7), где: Р1=4000 кгс; Р2=16000 кгс4 Р3=4000 кгс; α= ...

Разработка схемы учебного маршрута движения транспортного средства
Безопасное дорожное движение может осуществляться только высококвалифицированными водителями, обучение которых должно обеспечиваться применением эффективных средств и методов. Постоянно растущая интенсивность дорожного движения диктует необходимость проведения обучения вождению в условиях реальной ...