Аналитический обзор существующих методов и подходов к планированию групповых действий

При решении задач с помощью динамического программирования необходимо проделать три шага:

Разбиение задачи на подзадачи меньшего размера.

Нахождение решения подзадач рекурсивно, проделывая этот же алгоритм.

Использование полученного решения подзадач для конструирования решения глобальной задачи.

При этом каждая подзадача, в отличие, например, от метода полного перебора, решается только один раз и запоминается в специальной таблице. Значения из этой таблицы в дальнейшем используются при решении задач более высокого уровня.

При решении задачи поиска оптимального маршрута методом динамического программирования довольно часто используется алгоритм Дейкстры. Принцип работы этого алгоритма заключается в том, что каждый пункт маршрута ассоциируется с вершиной графа. Каждой вершине этого графа сопоставляется метка, значением которой является минимальное известное расстояние от начальной вершины до текущей. [2]

Рассмотрим выполнение алгоритма на примере графа, показанного на рисунке. Пусть требуется найти расстояния от 1-й вершины до всех остальных.

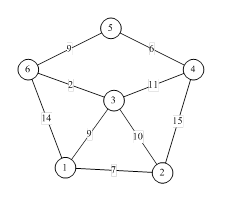
Рисунок 1.1.7 Представление задачи в виде графа

Кружками обозначены вершины, линиями – пути между ними (ребра графа). В кружках обозначены номера вершин, над ребрами обозначена их «цена» – длина пути. Рядом с каждой вершиной красным обозначена метка – длина кратчайшего пути в эту вершину из вершины 1.

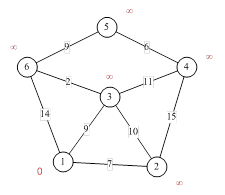
Рисунок 1.1.8 Введение меток для каждой вершины

Первый шаг. Рассмотрим шаг алгоритма Дейкстры для нашего примера. Минимальную метку имеет вершина 1. Её соседями являются вершины 2, 3 и 6. Первый по очереди сосед вершины 1 – вершина 2, потому что длина пути до неё минимальна. Длина пути в неё через вершину 1 равна кратчайшему расстоянию до вершины 1 + длина ребра, идущего из 1 в 2, то есть 0 + 7 = 7. Это меньше текущей метки вершины 2, поэтому новая метка 2-й вершины равна 7.

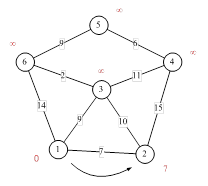
Рисунок 1.1.9

Аналогичную операцию проделываем с двумя другими соседями 1-й вершины – 3-й и 6-й.

Рисунок 1.1.10

Все соседи вершины 1 проверены. Текущее минимальное расстояние до вершины 1 считается окончательным и пересмотру не подлежит (то, что это действительно так, впервые доказал Дейкстра). Вычеркнем её из графа, чтобы отметить, что эта вершина посещена.

Второй шаг. Шаг алгоритма повторяется. Снова находим «ближайшую» из непосещенных вершин. Это вершина 2 с меткой 7.

Снова пытаемся уменьшить метки соседей выбранной вершины, пытаясь пройти в них через 2-ю. Соседями вершины 2 являются 1, 3, 4.

Первый (по порядку) сосед вершины 2 – вершина 1. Но она уже посещена, поэтому с 1-й вершиной ничего не делаем.

Следующий сосед вершины 2 – вершина 3. Если идти в неё через 2, то длина такого пути будет = 7 + 10 = 17. Но текущая метка третьей вершины равна 9<17, поэтому метка не меняется.

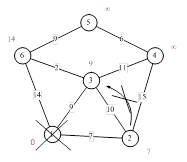
Рисунок 1.1.11

Ещё один сосед вершины 2 – вершина 4. Если идти в неё через 2-ю, то длина такого пути будет = кратчайшее расстояние до 2 + расстояние между вершинами 2 и 4 = 7 + 15 = 22. Поскольку 22<, устанавливаем метку вершины 4 равной 22.

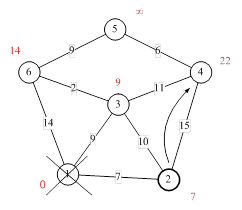
Рисунок 1.1.12

Все соседи вершины 2 просмотрены, замораживаем расстояние до неё и помечаем её как посещенную.

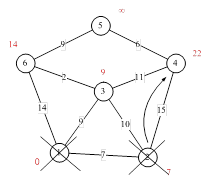
Рисунок 1.1.13

Третий шаг. Повторяем шаг алгоритма, выбрав вершину 3. После её «обработки» получим такие результаты:

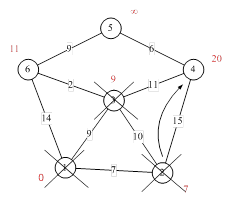
Рисунок 1.1.14

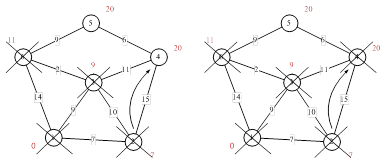
Дальнейшие шаги. Повторяем шаг алгоритма для оставшихся вершин (Это будут по порядку 6, 4 и 5).

Похожие статьи:

Оказание первой доврачебной помощи при поражении электрическим током, отравлении угарным газом, тепловом ударе, переломах, ожогах, открытых ранах
Поражение электрическим током - основной причиной несчастных случаев, обусловленных действием электрического тока, являются нарушения правил техники безопасности при работе с бытовыми электроприборами и промышленными электроустановками. Доврачебная помощь - одним из главных моментов при оказании пе ...

Договор морской перевозки по КТМ РФ2
В соответствии с морским законодательством Российской Федерации существуют два правовых режима: один - для морских перевозок между портами России (каботаж); другой - для перевозок в заграничном сообщении. Основное различие между ними заключается в том значении, которое придается воле сторон договор ...

Определение требований охраны труда и экологии окружающей среды
Участок, где постоянно производится дуговая и газовая сварка, должен иметь рабочую инструкцию, знание и выполнение которой обязательно для сварщиков, а так же должны быть вывешены плакаты, содержащие важнейшие указания по технике безопасности и пожарной безопасности. При производстве электросварочн ...